Teorema (Gauss, 1799). Todo polinomio no constante con coeficientes complejos posee al menos una raíz compleja.
Demostración. Sea
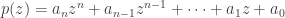
un polinomio de grado

con coeficientes complejos. La demostración se basa en la observación de que un punto

tal que

tiene la propiedad de que

alcanza su módulo mínimo en
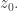
Veremos primero que efectivamente

alcanza su módulo mínimo en el plano complejo. Empezamos poniendo, para
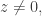
de modo que
Pongamos
Entonces, para todo

con
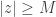
tenemos

y
de modo que
lo cual implica que
Esto significa que
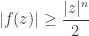
para

En particular, si
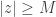
y también
![|z| \geq \sqrt[n]{2|f(0)|} |z| \geq \sqrt[n]{2|f(0)|}](http://s0.wp.com/latex.php?latex=%7Cz%7C+%5Cgeq+%5Csqrt%5Bn%5D%7B2%7Cf%280%29%7C%7D&bg=ffffff&fg=333333&s=0)
entonces
Ahora consideramos el conjunto cerrado y acotado
Supongamos que el módulo mínimo de

sobre

se alcanza en un cierto

de modo que

para todo

Se sigue, en particular, que
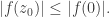
Así pues,
si
![|z| \geq \max (M, \sqrt[n]{2|f(0)|}) |z| \geq \max (M, \sqrt[n]{2|f(0)|})](http://s0.wp.com/latex.php?latex=%7Cz%7C+%5Cgeq+%5Cmax+%28M%2C+%5Csqrt%5Bn%5D%7B2%7Cf%280%29%7C%7D%29&bg=ffffff&fg=333333&s=0)
entonces

Combinando las anteriores desigualdades concluimos que

para todo

de modo que

alcanza su módulo mínimo sobre el plano complejo en
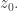
Para completar la demostración del teorema, ahora demostramos que

Resulta conveniente introducir la función

definida mediante
Entonces

es una función polifónica de grado

que alcanza su módulo mínimo en

Queremos probar que

Supongamos que, por el contrario,

Sea
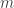
la menor potencia de

que aparece en la expresión de

de modo que
donde
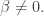
Ahora bien, todo número complejo no nulo tiene
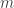
raíces
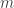
-ésimas, y por lo tanto existe

tal que
Poniendo entonces

tenemos
Esta expresión nos permitirá llegar rápidamente a una contradicción. Observamos primero que, eligiendo

suficientemente pequeño, tenemos
Si elegimos, entre todos los

para los que se verifica esta desigualdad, algún

real y positivo, entonces
En consecuencia, si

entonces
La contradicción ha llegado. Para tal número

tenemos
lo cual contradice el hecho de ser

el módulo mínimo de

sobre el plano complejo. Por lo tanto, la suposición original debe ser incorrecta y

Esto implica que

![|z| \geq \max (M, \sqrt[n]{2|f(0)|}) |z| \geq \max (M, \sqrt[n]{2|f(0)|})](http://s0.wp.com/latex.php?latex=%7Cz%7C+%5Cgeq+%5Cmax+%28M%2C+%5Csqrt%5Bn%5D%7B2%7Cf%280%29%7C%7D%29&bg=ffffff&fg=333333&s=0) entonces
entonces 
No hay comentarios.:
Publicar un comentario