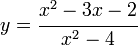Matemáticas IV : abril 2013

ejercicios función racional

Definición: Si P(x) y Q(x) son polinomios, la función de la forma:

se llama una función racional, donde Q(x) es diferente de cero.

Ejemplos:

El dominio de las funciones racionales es el conjunto de todos los números reales tal que el denominador sea diferente de cero.

Ejemplo para discusión: ¿Cuál es el dominio de cada una de las siguientes funciones?

Teorema: Sea f una función racional definida de la forma:

donde P(x) y Q(x) son polinomios. Si a es un número real que Q(a) = 0 y P(a) es diferente de cero, entonces la recta x = a es una asíntota vertical de la gráfica de y = f(x).

Ejemplos para discusión: Halla las asíntotas verticales para cada de las siguientes funciones:

Teorema: Sea f una función racional definida por el cociente de dos polinomios,

entonces:

1) Para m < n, la recta y = 0 (el eje x) es una asíntota horizontal.

2) Para m = n, la recta y = a_m/b_n, es una asíntota horizontal.

3) Para m > n, no hay asíntotas horizontales.

Ejemplos para discusión: Halla las asíntotas horizontales para cada una de las siguientes funciones:

Gráfica de funciones racionales

Ahora utilizaremos las técnicas de interceptos y asíntotas para graficar algunas funciones racionales.

Ejemplos para discusión: Dibuja la gráfica de:

Ejercicio de práctica: Halla las asíntotas verticales y horizontales para cada una de las siguientes funciones. Dibuja la gráfica.

Teorema: Si f es una función definida de la forma:

donde P(x) y Q(x) son polinomios y el grado de P(x) es 1 más que el grado de Q(x), entonces se puede expresar de la forma:

donde el grado de r(x) es menor que el grado de Q(x). La recta y = mx + b es una asíntota oblicua para la gráfica de f.

Ejemplo para discusión: Halla las asíntotas verticales, horizontales y oblicuas para:

Dibuja la gráfica.

Ejercicio de práctica: Halla las asíntotas verticales, horizontales y oblicuas para:

función racional

En matemáticas, una función racional es una función que puede ser expresada de la forma:

$f(x) = \frac{P(x)}{Q(x)}$

donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición en todos los valores de x que no anulen el denominador.¹
La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.
Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.

Función racional de grado 2:

$y = \cfrac{x^2 -3x -2}{x^2 -4}$

Función racional de grado 3:

$y = \cfrac{x^3 -2x}{2(x^2 -5)}$

teorema de factorización

FACTORIZACIÓN DE POLINOMIOS

Para factorizar polinomios hay varios métodos:

Sacar factor común: Es aplicar la propiedad distributiva de la multiplicación respecto de la suma, Así, la propiedad distributiva dice:

Pues bien, si nos piden factorizar la expresión , basta aplicar la propiedad distributiva y decir que

Cuando nos piden sacar factor común o simplemente factorizar y hay coeficientes con factores comunes, se saca el máximo común divisor de dichos coeficientes. Por ejemplo, si nos piden factorizar la expresión , será

donde 6 es el máximo común divisor de 36, 12 y 18

Para comprobar si la factorización se ha hecho correctamente, basta efectuar la multiplicación, aplicando la propiedad distributiva de la parte derecha de la igualdad, y nos tiene que dar la parte izquierda.

Otro ejemplo: Factorizar

¡Atención a cuando sacamos un sumando completo!, dentro del paréntesis hay que poner un uno. Tener en cuenta que si hubiéramos puesto y quiero comprobar si está bien, multiplico y me da pero no como me tendría que haber dado.

Sin embargo si efectúo

Otros ejemplos:

Si se trata de una diferencia de cuadrados: Es igual a suma por diferencia.

Se basa en la siguiente fórmula

Pero aplicada al revés, o sea que si me dicen que factorice escribo

Otros ejemplos de factorización por este método:

Si se trata de un trinomio cuadrado perfecto: Es igual al cuadrado de un binomio

Se basa en las siguientes fórmulas

Así si nos dicen que factoricemos: , basta aplicar la fórmula anterior y escribir que

teorema fundamental del algebra

Teorema (Gauss, 1799). Todo polinomio no constante con coeficientes complejos posee al menos una raíz compleja.
Demostración. Sea $p(z)=a_nz^n + a_{n-1}z^{n-1} + \cdots + a_1z+a_0$ un polinomio de grado $n \geq 1$ con coeficientes complejos. La demostración se basa en la observación de que un punto $z_0 \in \mathbb{C}$ tal que $f(z_0)=0$ tiene la propiedad de que $f$ alcanza su módulo mínimo en $z_0.$ Veremos primero que efectivamente $f$ alcanza su módulo mínimo en el plano complejo. Empezamos poniendo, para $z \neq 0,$

$\displaystyle{f(z)=z^n \left (1+ \frac{a_{n-1}}{z} + \cdots + \frac{a_0}{z^n} \right ),}$

de modo que

$\displaystyle{|f(z|)=|z|^n \cdot \left | 1+ \frac{a_{n-1}}{z} + \cdots + \frac{a_0}{z^n} \right |,}$

Pongamos

$M = \max \{1, 2n |a_{n-1}|, \ldots , 2n |a_0| \}.$

Entonces, para todo $z$ con $|z| \geq M$ tenemos $|z^k| \geq |z|\;$ y

$\displaystyle{\frac{|a_{n-k}|}{|z^k|} \leq \frac{|a_{n-k}|}{|z|} \leq \frac{|a_{n-k}|}{2n|a_{n-k}|}=\frac{1}{2n},}$

de modo que

$\displaystyle{\left | \frac{a_{n-1}}{z} + \cdots + \frac{a_0}{z^n} \right | \leq \left | \frac{a_{n-1}}{z} \right | + \cdots + \left | \frac{a_0}{z^n} \right | \leq \frac{1}{2},}$

lo cual implica que

$\displaystyle{\left | 1+ \frac{a_{n-1}}{z} + \cdots + \frac{a_0}{z^n} \right | \geq 1- \left | \frac{a_{n-1}}{z} + \cdots + \frac{a_0}{z^n} \right | \geq \frac{1}{2}.}$

Esto significa que

$\displaystyle{|f(z)| \geq \frac{|z|^n}{2}}$ para $|z| \geq M.$

En particular, si $|z| \geq M$ y también $|z| \geq \sqrt[n]{2|f(0)|}$ entonces

$|f(z)| \geq |f(0)|.$

Ahora consideramos el conjunto cerrado y acotado

$K=\{z \in \mathbb{C}: |z| \leq \max (M, \sqrt[n]{2|f(0)|}) \}.$

Supongamos que el módulo mínimo de $f$ sobre $K$ se alcanza en un cierto $z_0 \in K,$ de modo que

$|f(z_0) | \leq |f(z)|$ para todo $z \in K.$

Se sigue, en particular, que $|f(z_0)| \leq |f(0)|.$ Así pues,

si $|z| \geq \max (M, \sqrt[n]{2|f(0)|})$ entonces $|f(z)| \geq |f(0)| \geq |f(z_0)|.$

Combinando las anteriores desigualdades concluimos que $|f(z_0)| \leq |f(z)|$ para todo $z \in \mathbb{C},$ de modo que $f$ alcanza su módulo mínimo sobre el plano complejo en $z_0.$
Para completar la demostración del teorema, ahora demostramos que $f(z_0)=0.$ Resulta conveniente introducir la función $g$ definida mediante

$g(z)=f(z+z_0).$

Entonces $g$ es una función polifónica de grado $n$ que alcanza su módulo mínimo en $0.$ Queremos probar que $g(0)=0.$ Supongamos que, por el contrario, $g(0) \neq 0.$ Sea $m$ la menor potencia de $z$ que aparece en la expresión de $g(z),$ de modo que

$g(z)= \alpha + \beta z^m + c_{m+1}z^{m+1} + \cdots + c_n z^n,$

donde $\beta \neq 0.$ Ahora bien, todo número complejo no nulo tiene $m$ raíces $m$ -ésimas, y por lo tanto existe $\gamma \in \mathbb{C}$ tal que

$\displaystyle{\gamma^n = -\frac{\alpha}{\beta}.}$

Poniendo entonces $d_k=\gamma^kc_k$ tenemos

$|g(\gamma z)|= |\alpha + \beta \gamma^m z^m + d_{m+1}z^{m+1} + \cdots + d_n z^n|$

$\displaystyle{= |\alpha - \alpha z^m + d_{m+1}z^{m+1} + \cdots |}$

$\displaystyle{= \left | \alpha \left (1-z^m+ \frac{d_{m+1}}{\alpha} z^{m+1} + \cdots \right ) \right |}$

$\displaystyle{= \left | \alpha \left (1-z^m+ z^m \left [ \frac{d_{m+1}}{\alpha}z + \cdots \right ] \right ) \right |}$

$\displaystyle{=|\alpha| \cdot \left | 1-z^m+ z^m \left [ \frac{d_{m+1}}{\alpha}z + \cdots \right ]\right |.}$

Esta expresión nos permitirá llegar rápidamente a una contradicción. Observamos primero que, eligiendo $|z|$ suficientemente pequeño, tenemos

$\displaystyle{\left | \frac{d_{m+1}}{\alpha}z + \cdots \right | <1.}$

Si elegimos, entre todos los $z$ para los que se verifica esta desigualdad, algún $z$ real y positivo, entonces

$\displaystyle{\left | z^m \left [ \frac{d_{m+1}}{\alpha}z + \cdots \right ] \right | <|z^m|=z^m.}$

En consecuencia, si $0 < z < 1$ entonces

$\displaystyle{\left | 1-z^m+ z^m \left [ \frac{d_{m+1}}{\alpha}z + \cdots \right ] \leq \right |}$

$\displaystyle{\leq |1-z^m| + \left | z^m \left [ \frac{d_{m+1}}{\alpha}z + \cdots \right ] \right |=}$

$\displaystyle{= 1-z^m + \left | z^m \left [ \frac{d_{m+1}}{\alpha}z + \cdots \right ] \right | <}$

$\displaystyle{<1-z^m+z^m=1.}$

La contradicción ha llegado. Para tal número $z$ tenemos

$|g(\gamma z)| < |\alpha|,$

lo cual contradice el hecho de ser $|\alpha|$ el módulo mínimo de $g$ sobre el plano complejo. Por lo tanto, la suposición original debe ser incorrecta y $g(0)=0.$ Esto implica que $f(z_0)=0.$

domingo, 28 de abril de 2013

ejercicios función racional

función racional

teorema de factorización

teorema fundamental del algebra