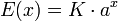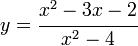Utilizas funciones exponenciales y logarítmicas

función exponencial

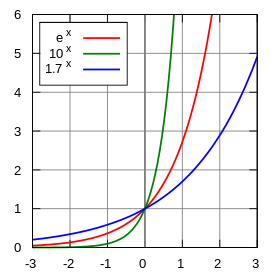
La función exponencial, es conocida formalmente como la función real e^x, donde e es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=e^x o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.

En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma

siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base aque utilicen.

Función logarítmica 

Para justificar la definición de logaritmos, es necesario mostrar que la ecuación

tiene una solución x y que esta solución es única, provista de que y es positivo y que b es positivo y distinto de 1. Una demostración de este hecho requiere del teorema del valor intermedio delcálculo elemental.³ Este teorema establece que una función continua que produce dos valores m y n también produce cualquier valor que se encuentre entre m y n. Una función es continua si esta no «salta», esto es, si su gráfico puede ser escrito sin levantar el lápiz del papel.

Esta propiedad se puede demostrar que se cumple para la función f(x) = b^x. Puesto que f toma arbitrariamente valores grandes positivos y valores pequeños positivos, cualquier número y > 0 que se encuentra entre f(x₀) y f(x₁) para un adecuado x₀ y x₁. Por lo tanto, el teorema del valor intermedio asegura que la ecuación f(x) = y tiene una solución. Más aún, hay únicamente una solución para esta ecuación, puesto que la función f es estrictamente creciente (para b > 1), o estrictamente decreciente (para 0 < b < 1).⁴

La única solución x es el logaritmo de y en la base b, log_b(y). La función que asigna a cada y su logaritmo se llama función logaritmo o función logarítmica (o logaritmo a secas).

Propiedades de los exponentes

Propiedades de los exponentes

1.- b^m bⁿ = b^n+m
En el producto con bases iguales se suman los exponentes. 
Ejemplo: 2² 2³ = 2^{2 + 3} = 2⁵ = 32

·        

2.-(b^m )ⁿ = b^{n m}Una base con doble exponente; se multiplican los exponentes.
Ejemplo: (3³)² = 3 ^{3 x 2} = 3⁶ = 729

·         

3.-(ab)ⁿ = aⁿ bⁿ
Un producto elevado a un exponente; cada factor se eleva a ese exponente. 
Ejemplo: (7x)² = 7²x ² = 49x²

·       

4.-
En el cociente con bases iguales se restan los exponentes.
Ejemplo: 

·      

5.-  
Un cociente elevado a un exponente; cada término se eleva a ese exponente.
Ejemplo: 

·     






  6.- 
Un cociente con exponente negativo es el recíproco del cociente positivo.
Ejemplo: 

·         7.-
Un cociente con exponente negativo es el recíproco del cociente positivo.
Ejemplo: 

Definición de logaritmo

De la definición de logaritmo podemos deducir:

No existe el logaritmo de un número con base negativa.

No existe el logaritmo de un número negativo.

No existe el logaritmo de cero.

El logaritmo de 1 es cero.

El logaritmo en base a de a es uno.

El logaritmo en base a de una potencia en base a es igual al exponente.

Propiedades de los logaritmos

1El logaritmo de un producto es igual a la suma de los logaritmos de los factores.

2 El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor.

3El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base.

4El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz.

• 

5Cambio de base:

 

Ecuación exponencial

Una ecuación exponencial es aquella ecuación en la que la incógnita aparece en el exponente.

Para resolver una ecuación exponencial vamos a tener en cuenta:

1

2

3 Las propiedades de las potencias.

a⁰ = 1 ·

a¹ = a

a^m · a ⁿ = a^m+n

a^m : a ⁿ = a^{m - n}

(a^m)ⁿ = a^{m · n}

aⁿ · b ⁿ = (a · b) ⁿ

aⁿ : b ⁿ = (a : b) ⁿ    

 Las ecuaciones logarítmicas son aquellas ecuaciones en la que la incógnita aparece afectada por un logaritmo.

Para resolver ecuaciones logarítmicas vamos a tener en cuenta:

1 Las propiedades de los logaritmos.

2 

3 

4 Además tenemos que comprobar las soluciones para verificar que no tenemos logaritmos nulos o negativos.

ejercicios función racional

Definición:  Si P(x)  y  Q(x) son polinomios, la función de la forma:

se llama una función racional, donde Q(x) es diferente de cero.

Ejemplos:

El dominio de las funciones racionales es el conjunto de todos los números reales tal que el denominador sea diferente de cero.

Ejemplo para discusión:  ¿Cuál es el dominio de cada una de las siguientes funciones?

Teorema:  Sea f una función racional definida de la forma:

donde P(x)  y  Q(x) son polinomios.  Si a es un número real que Q(a) = 0 y  P(a) es diferente de cero, entonces  la recta  x = a  es  una  asíntota  vertical  de la gráfica de  y = f(x).

Ejemplos para discusión:  Halla las asíntotas verticales para cada de las siguientes funciones:

Teorema:  Sea f una función racional definida por el cociente de dos polinomios,

entonces:

1) Para m < n,  la recta y = 0 (el eje x) es una asíntota horizontal.

2) Para m = n, la recta  y = a_m/b_n, es una asíntota horizontal.

3) Para m > n,  no hay asíntotas horizontales.

Ejemplos para discusión:  Halla las asíntotas horizontales para cada una de las siguientes funciones:

Gráfica de funciones racionales

 Ahora utilizaremos las técnicas de interceptos y asíntotas para graficar algunas funciones racionales.

Ejemplos para discusión:  Dibuja la gráfica de:

Ejercicio de práctica:  Halla las asíntotas verticales y horizontales para cada una de las siguientes funciones.  Dibuja la gráfica.

Teorema:  Si f es una función definida de la forma:

donde P(x)  y  Q(x) son polinomios y el grado de P(x) es 1 más que el grado de Q(x), entonces se puede expresar de la forma:

donde el grado de r(x) es menor que el grado de Q(x).  La recta y = mx + b es una asíntota oblicua para la gráfica de f.

Ejemplo para discusión:  Halla las asíntotas verticales, horizontales y oblicuas para:

Dibuja la gráfica.

Ejercicio de práctica: Halla las asíntotas verticales, horizontales y oblicuas para:

función racional

En matemáticas, una función racional es una función que puede ser expresada de la forma:

donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición en todos los valores de x que no anulen el denominador.¹
La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.
Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.

Función racional de grado 2:

Función racional de grado 3: